7주차 암호학

이산 로그 문제(Discrete Logarithm Problem)

자연수 a,m, 정수 b에 대해 a^x≡b(modm)을 만족하는 정수 x를 구하는 문제이다

 

Diffie-Hellman 키 교환

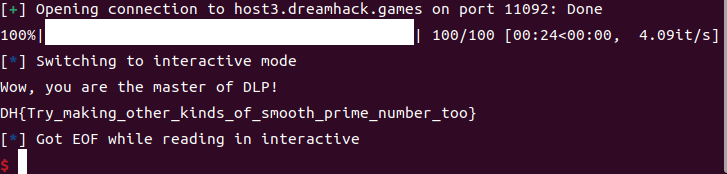
1976년 Whitfield Diffie와 Martin Hellman은 공개된 채널로 키를 교환할 수 있는 Diffie-Hellman 키 교환 절차를 만들어냈다. 예시를 들어 설명해보겠다. 키 교환에서 통신을 진행하는 가상의 두 인물을 Alice와 Bob이라고 한다. 둘 사이에서는 다음의 절차에 따라 교환이 이루어진다. 

 

1. 키를 교환하고자 하는 Alice는 소수 p와 1≤g≤p−1을 만족하는 적당한 수 g를 정해 Bob에게 전송합니다. p는 보통 2^1024 이상의 큰 소수로 설정합니다.

 

2. 다시 Alice는 1≤a≤p−1을 만족하는 적당한 수 a를 정하여 A=g^a mod p를 Bob에게 전송합니다.

 

3. Alice로 부터 g와 p를 받은 Bob은 1≤b≤p−1을 만족하는 적당한 수 b를 정해 B=g^b modp를 Alice에게 전송합니다.

 

4. Alice는 Bob이 보낸 B를 a제곱하여 K≡B^a≡(g^b)^a≡g^(ba) mod p를 계산하고, Bob은 Alice가 보낸 A를 b제곱하여 K≡A^b≡(g^a)^b≡g^(ab) mod p를 계산합니다. Alice와 Bob은 계산한 K를 통신의 키로 사용하게 됩니다.

Diffie-Hellman에 대한 중간자 공격

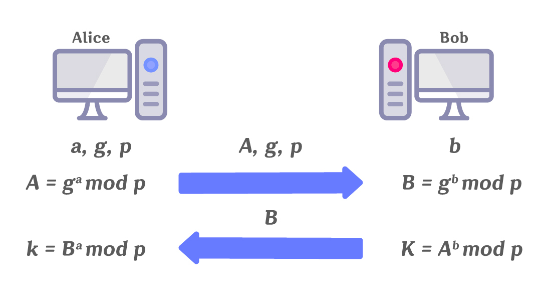
네트워크로 통신하는 두 주체는 서로의 신원을 확인하기 어렵다. 중간자 공격(Man-In-The-Middle attack, MITM)은 네트워크의 이런 특성을 이용한 공격이다. 중간자 공격은 능동적 공격으로 통신을 도청하면서 중간에 데이터를 위변조할 수 있다. 

 

먼저, Alice와 Bob이 통신할 때, 공격자는 Alice에게 자신을 Bob이라고, 그리고 Bob에게는 자신을 Alice라고 속인다. Alice와 Bob은 통신하는 상대방이 공격자인지, 아니면 신뢰하는 상대방인지 알 수 없다.

challenge.py

#!/usr/bin/python3
from Crypto.Util.number import getPrime
from Crypto.Util.Padding import pad, unpad
from Crypto.Cipher import AES
import hashlib
import random

class Person(object):
    def __init__(self, p):
        self.p = p
        self.g = 2
        self.x = random.randint(2, self.p - 1)
    
    def calc_key(self):
        self.k = pow(self.g, self.x, self.p)
        return self.k

    def set_shared_key(self, k):
        self.sk = pow(k, self.x, self.p)
        aes_key = hashlib.md5(str(self.sk).encode()).digest()
        self.cipher = AES.new(aes_key, AES.MODE_ECB)

    def encrypt(self, pt):
        return self.cipher.encrypt(pad(pt, 16)).hex()

    def decrypt(self, ct):
        return unpad(self.cipher.decrypt(bytes.fromhex(ct)), 16)

flag = open("flag", "r").read().encode()
prime = getPrime(1024)
print(f"Prime: {hex(prime)}")
alice = Person(prime)
bob = Person(prime)

alice_k = alice.calc_key()
print(f"Alice sends her key to Bob. Key: {hex(alice_k)}")
print("Let's inturrupt !")
alice_k = int(input(">> "))
if alice_k == alice.g:
    exit("Malicious key !!")
bob.set_shared_key(alice_k)

bob_k = bob.calc_key()
print(f"Bob sends his key to Alice. Key: {hex(bob_k)}")
print("Let's inturrupt !")
bob_k = int(input(">> "))
if bob_k == bob.g:
    exit("Malicious key !!")
alice.set_shared_key(bob_k)

print("They are sharing the part of flag")
print(f"Alice: {alice.encrypt(flag[:len(flag) // 2])}")
print(f"Bob: {bob.encrypt(flag[len(flag) // 2:])}")

해당 문제를 해결하는 방법은 악의적인 값을 송신하는 방법도 있지만 저는 특수한 값을 송신하는 걸로 했습니다. 0은 얼마를 거듭제곱하여도 0의 결과를 가지고, 1도 동일한 성질을 가지고 있습니다. 따라서 0 또는 1을 송신하게 되면 Alice, Bob의 키가 0 또는 1로 설정되는 걸 이용했습니다.

from pwn import *
from Crypto.Util.Padding import pad, unpad
from Crypto.Cipher import AES
import hashlib

def decrypt(shared, ciphertext):
    aes_key = hashlib.md5(str(shared).encode()).digest()
    cipher = AES.new(aes_key, AES.MODE_ECB)

    return unpad(cipher.decrypt(ciphertext), 16)

io = remote("host3.dreamhack.games", 9957)

io.sendlineafter(">> ", b"0")
io.sendlineafter(">> ", b"0")

io.recvuntil(b"Alice: ")
flag1 = decrypt(0, bytes.fromhex(io.recvline().decode()))

io.recvuntil(b"Bob: ")
flag2 = decrypt(0, bytes.fromhex(io.recvline().decode()))

io.close()

print((flag1 + flag2).decode())

 

 

chall.py

from Crypto.Util.number import isPrime
import secrets

flag = open("flag.txt", "r").read()

pbits = 512

p = int(input("Prime: "))
g = int(input("g: "))
assert isPrime(p) and p.bit_length() == pbits

for rnd in range(100):
    print(f"--- Round {rnd + 1} ---")
    secret = secrets.randbits(pbits)
    print(f"{pow(g, secret, p) = }")
    assert secret == int(input("secret: "))

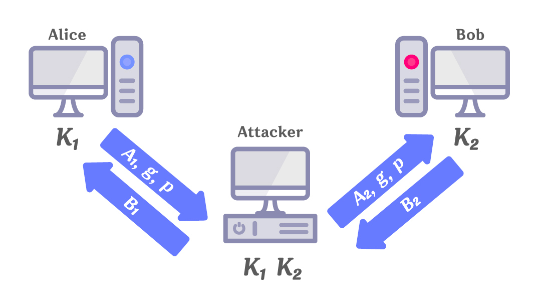
print("Wow, you are the master of DLP!")
print(flag)

문제를 해결하기 위해서는

1. p−1를 소인수분해 했을 때, 작은 소인수만으로 구성되어야 한다. 즉, 작은 수 B에 대해서 B-smooth 해야 한다.
2. 100회 연속 이산 로그 문제를 해결할 수 있어야 한다.

이 조건을 만족하는 512비트 소수 p를 찾아야한다. 

 

익스플로잇 설계

p−1가 Smooth한 수일 때 g와 g^k mod p로부터 k를 빠른 시간 내에 구할 수 있음에 앞서, g의 Multiplicative order이라는 개념을 정리해야 할 필요가 있다.

 

페르마의 소정리에 의하면, p와 서로소인 어떤 정수 g에 대해서도 g^(p−1)≡1(mod p)를 만족한다. 따라서 모든 1 이상 p−1 이하의 정수 g에 대하여 p−1회 곱하면 곱셈의 항등원인 1의 결과가 나온다. 정수 g의 Multiplicative order은 항등원 1이 되기까지 곱해야 하는 최소 횟수로 정의페르마의 소정리에 의하면 [1,p)에 속하는 모든 정수 g에 대하여 g의 Multiplicative order은 p−1로 추정되지만, 실제로는 그렇지 않다.

from sage.all import *
from pwn import *
from Crypto.Util.number import isPrime
from tqdm import trange

# io = process(["python3", "chall.py"])
io = remote("host3.dreamhack.games", "15789")

pbits = 512

base = 1
for small_p in Primes():
    base *= small_p
    if int(base).bit_length() >= pbits - 20:  # SageMath 정수를 Python 정수로 변환
        break

k = 2**pbits // base
p = k * base + 1

while not isPrime(int(p)):  # SageMath 정수를 Python 정수로 변환
    p -= base

Fp = GF(p)
g = Fp.multiplicative_generator()

io.sendlineafter(b": ", str(p).encode())
io.sendlineafter(b": ", str(g).encode())

for _ in trange(100):
    io.recvuntil(b"= ")
    res = int(io.recvline())
    secret = Fp(res).log(g)
    
    io.sendlineafter(b": ", str(secret).encode())

io.interactive()