최대공약수(Greatest Common Divisor, GCD)는 둘 이상의 주어진 수들에 대하여 공약수, 즉 모든 주어진 수들의 공통의 약수인 수들 중에서 가장 큰 값을 의미한다.
유클리드 호제법이라고도 불리는 유클리드 알고리즘(Euclidean algorithm)은 소인수분해 과정 없이도 두 수의 최대공약수를 구할 수 있는 방법입니다.
서로소는 특별히 양의 정수 의 최대공약수의 값이 1인 경우를 표현합니다.
합동은 두 정수 를 각각 양의 정수 으로 나눈 나머지가 동일할 경우, “는 에 대하여 합동” 이라고 표현합니다.
위의 표현은 다음과 같이 수식으로 작성할 수 있습니다. 합동 관계를 작성한 수식을 합동식(Congruence relation)이라고 부릅니다.

합동식과 관련하여 암호학에 관련하여 중요한 몇 가지가 있습니다.

꼴의 합동식에서 을 법(Modulus)이라고 부른다.
덧셈의 항등원과 역원
Modulus 위에서 덧셈에 대한 항등원은 일반적인 덧셈에 대한 항등원과 동일한 0입니다. 물론, 등과 같이 표현 가능하지만, 모두 으로 나눈 나머지는 0으로 동일하므로 생략하겠습니다.
역원 또한 간단히 계산 가능합니다. 에 대한 역원은 , 를 포함해 와 같은 값들이 될 수 있습니다. 단, 이 값들은 Modulus 위에서 모두 동일합니다.
곱셈의 항등원과 역원
Modulus 위에서 곱셈에 대한 항등원은 일반적인 곱셈에 대한 항등원과 동일한 1입니다.
그러나 역원의 경우 상황에 따라 존재하거나 존재하지 않을 수도 있습니다.
의 역원 이 존재한다고 가정하면, 다음의 식이 성립하여야 합니다.
중국인의 나머지 정리(Chinese Remainder Theorem, CRT) 는 서로소인 두 Modulus 위에서 각각 의 값이 유일하게 정해지는 경우, 는 modulus 위에서 의 modulus 위에서 항상 유일하게 해가 존재한다.
Exponentiation by squaring은 큰 지수에 대한 거듭제곱을 연산할 때 사용되는 방법다. 여러 가지 방법이 존재하고, 종류에 따라 Square-and-multiply, Binary exponentiation 등의 이름들 또한 존재한다.
Python의 내장 pow 함수는 modulus 위에서의 거듭제곱을 연산해주는 함수입니다. pow(n, e, m)의 결과는 modulus 위에서의 값을 계산해줍니다
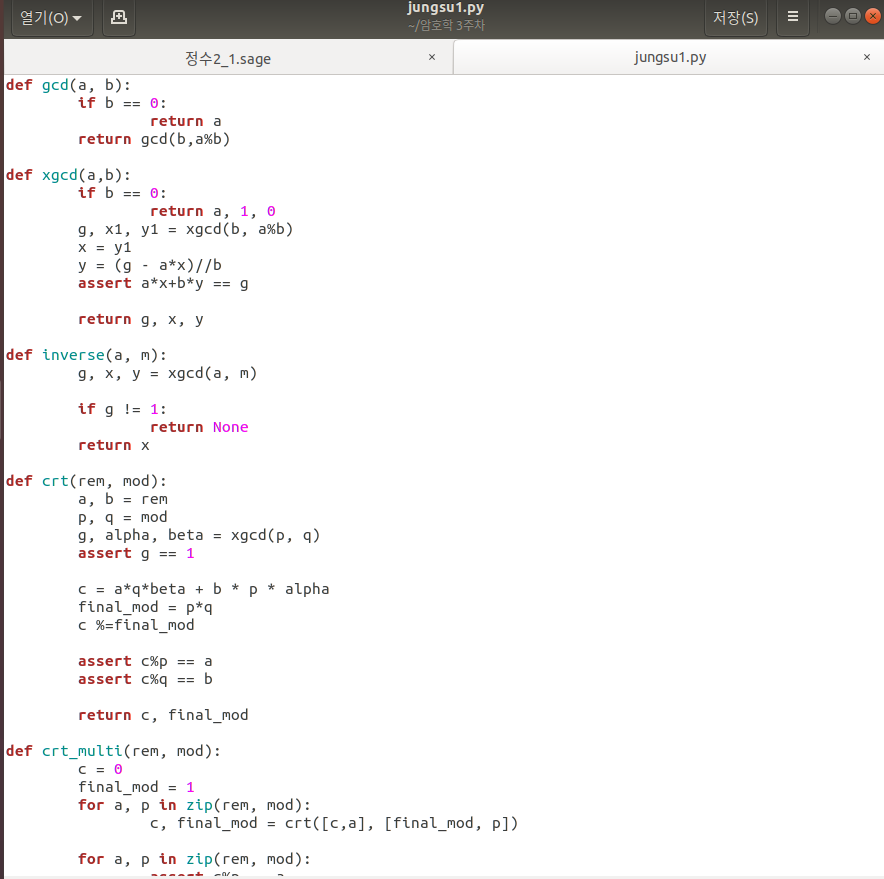
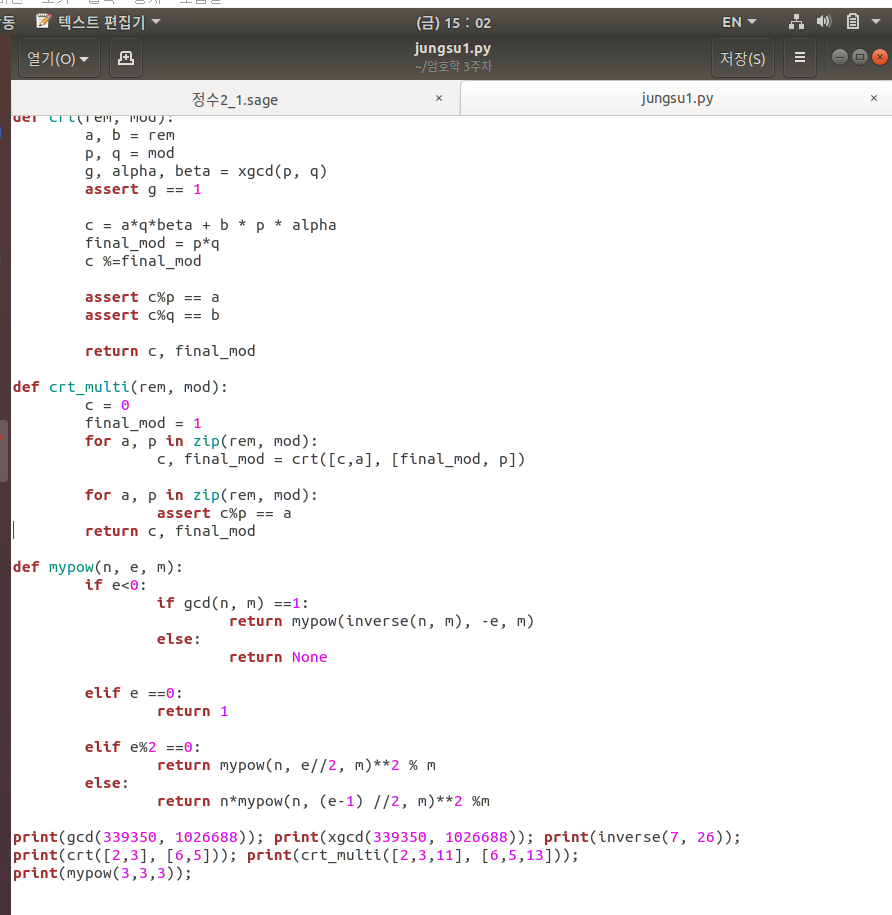
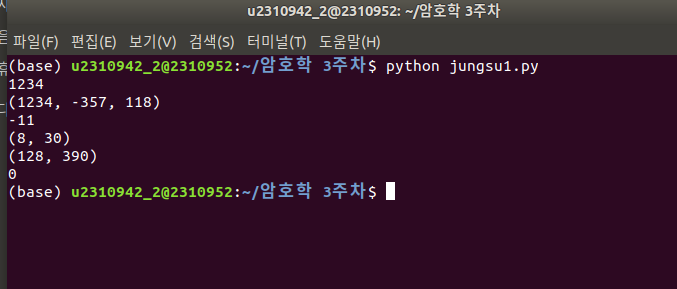
드림핵의 mypow의 숫자가 커서 3, 3, 3으로 대체했습니다.
페르마의 소정리
소수(Prime number)가 가지는 여러 중요한 성질 중 하나에 관한 정리입니다.

페르마의 소정리는 소수가 가지는 중요한 성질로서, 소인수분해 알고리즘이나 소수 판별법에서 중요한 역할을 합니다.
오일러 정리
오일러 정리(Euler’s theorem)는 양의 정수 과 서로소인 양의 정수 이 다음 식을 만족한다는 정리입니다.
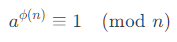
여기서 는 오일러 파이 함수(Euler's phi function)라고 불리며, n 이하의 양의 정수 중에서 n과 서로소인 수의 개수를 의미한다.
sage 실습


위와 같이 입력할 시

이런 오류가 드림핵처럼 출력되는 걸 확인할 수 있다.

sage에 pycryptodome를 설치해줍니다.

GF 클래스
갈루아 필드(Galois Field)라고도 불리는 유한체(Finite Field)의 앞 글자를 따와서 정의된 클래스다. GF 클래스도 간단한 연산들에 대해서는 SageMath에서 GF(q)와 같이 사용 가능한다.

벡터
환(Ring) 위의 원소들이 차원 수만큼 나열되어 이루어지는 물리량이다. 덧셈과 뺄셈, 스칼라 곱셈, 내적 곱셈이 가능하다.
스칼라곱셈의 예시는 아래와 같다.


내적 곱셈의 예시는 아래와 같다.

정리하자면 이렇다.


sageMath에서 실습한 내용이다.
행렬
환 위의 원소들을 직사각형 모양으로 배열한 것입니다. 행렬은 한자어 行列에서 비롯되었고, 행과 열을 붙여 만들어진 단어이다.
예시를 들면 이렇게 생겼다.

행은 가로줄이고 열은 세로줄이다.


행렬의 크기:행렬의 높이*열의 개수이다. M은 3*5이다.

Matrix(n,m)을 이용하여 행렬을 생성할 수 있다.
행렬과 벡터는 곱할 수 있다. 내적 곱셈하기 위해서는 같은 환 위에서 정의되어야 하는 것 뿐만 아니라, 두 벡터가 같은 차원을 가지고 있어야 한다는 조건까지 충족되어야 한다.

전자의 경우 곱셈이 가능하지만 후자의 경우는 불가능하다.


위와 같은 과정으로 곱셈이 이루어진다.

선형 방정식은 위와 같이 서술한다.



연립 선형 합동식은 아래와 같다.

연립 선형 방정식은 행에 각 숫자들을 곱하거나 나누어 다른 행에 더하거나 뺀다.
- 두 식의 순서 바꾸기
- 한 식에 특정 값을 곱하거나 나누기
- 한 식에서 다른 식에 특정 값을 곱하여 더하거나 빼기
이것을 할 수 있다. 기본행연산법은 위와 같은 과정으로 이루어진다.
행사다리꼴행렬(Row echelon form 행렬)
행렬 방정식의 해를 구하기 간편한 꼴의 행렬입니다. 모든 행렬은 기본행연산법을 통해 행사다리꼴행렬로 만들 수 있습니다. m*n크기의 행사다리꼴행렬일 필요충분 조건은 다음과 같다.

이를 가우스 소거법을 이용하여 계산한다.


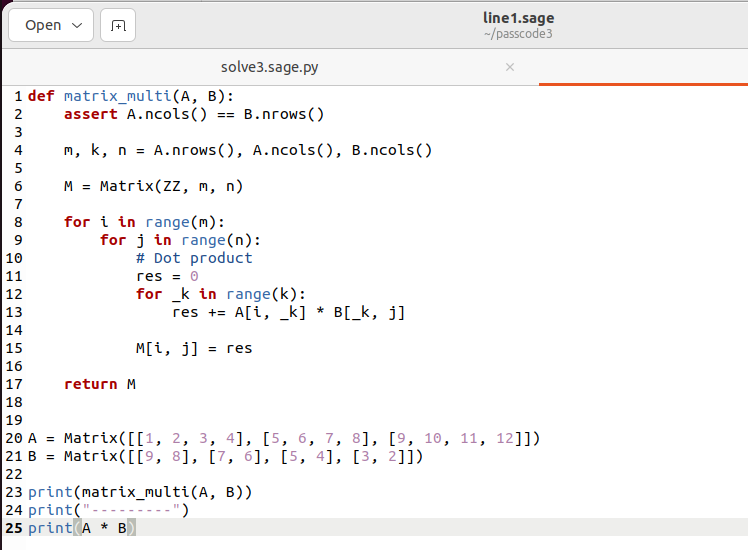

행렬과 행렬 사이도 곱셈이 가능하다. 크기의 행렬 와 크기의 행렬 에 대하여 는 크기의 행렬이다.
기약행사다리꼴행렬(Reduced row echelon form, RREF 행렬)은 행렬 방정식의 해를 바로 구할 수 있는 꼴의행렬입니다. 가우스 조던 소거법을 이용하여 구한다.


solve_right과 역행렬
SageMath의 Matrix 클래스에 존재하는 메서드 함수 solve_right은 크기의 행렬 과 차원의 벡터 에 대하여 를 만족하는 차원 벡터 를 찾을 수 있는 함수다. 이 조건을 만족하는 해가 존재하지 않는다면 ValueError Exception을 내고, 해가 존재한다면 그 중 하나의 해를 반환해다.


정사각행렬은 행의 수와 열의 수가 같은 행렬로, 등이 정사각행렬의 예시입니다. 크기의 정사각행렬 여러 개를 여러 번 곱하더라도 결과는 그대로의 크기를 가지고 있다는 특징을 가지고 있다. 따라서 크기의 정사각행렬은 곱셈에 대해 닫혀 있다.
크기의 정사각행렬 에 대하여, 을 만족하는 크기의 정사각행렬 을 의 역행렬(Inverse matrix)이라고 한다. 이 곱셈에서의 항등원이기 때문에, 은 의 곱셈의 역원과 같다.


solve코드


플래그 획득
